本文主要介绍函数的y=39x³+73lnx的定义域、单调性、凸凹性、极限等性质，并通过导数计算函数的单调区间和凸凹区间，同时简要画出函数的示意图。

方法/步骤

1

函数的定义域：根据函数特征，对于对数lnx，有x>0，所以本题函数的定义域为：（0，+∞）。



2

形如y=f(x)，则x是自变量，它代表着函数图像上每一点的横坐标，自变量的取值范围就是函数的定义域。f是对应法则的代表，它可以由f(x)的解析式决定。

3

函数的单调性，通过函数的一阶导数，求出函数的单调区间。



4

如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加;反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。

5

计算函数的二阶导数，得到函数的拐点，根据拐点的符号，解析函数的凸凹性，进而求解函数的凸凹区间。



6

如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立，那么在区间I上f(x)的图像上的任意两点连出的一条线段，这两点之间的函数图像都在该线段的下方，反之在该线段的上方。

7

函数上的部分点，函数五点图表如下：



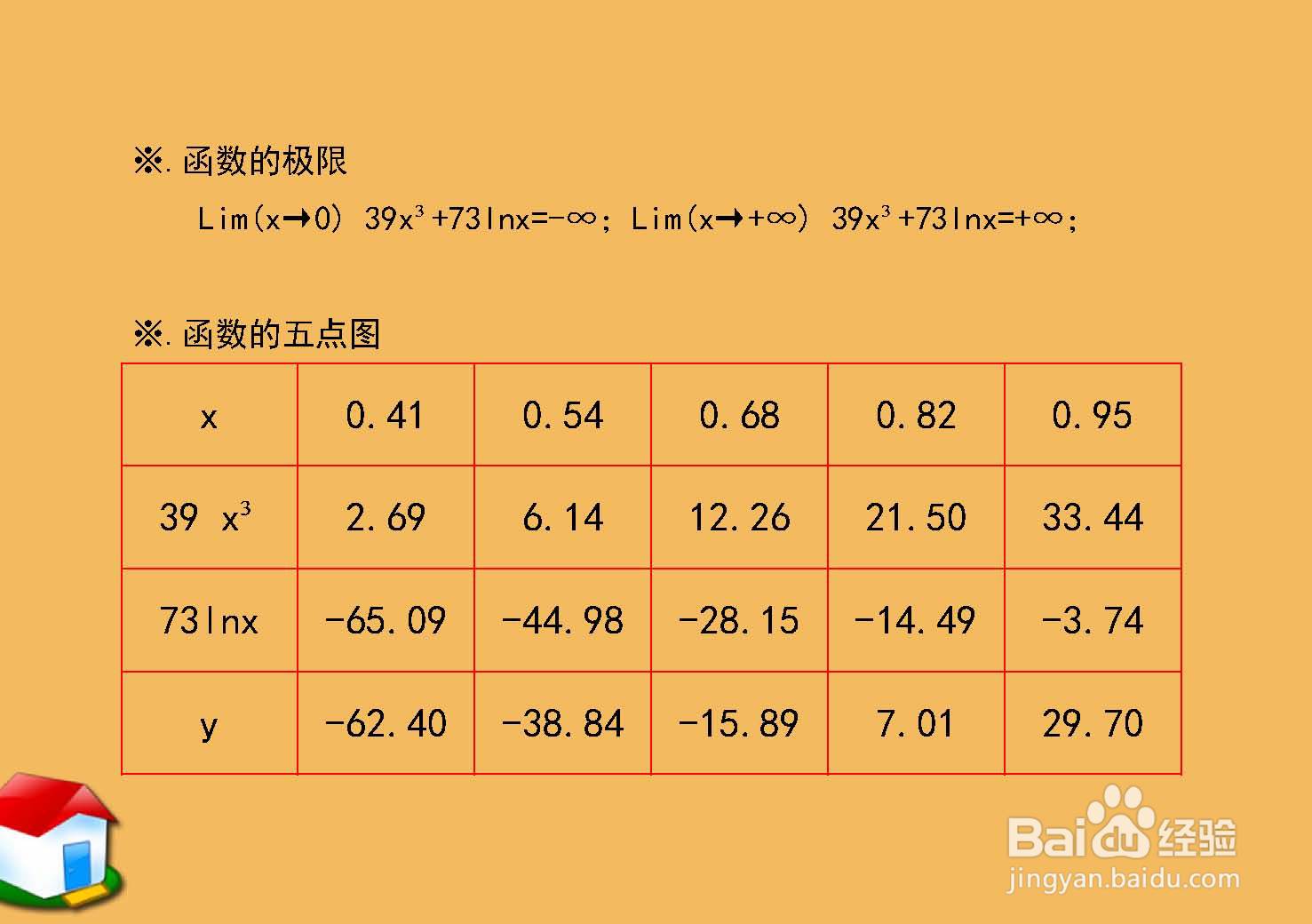
8

综合以上函数的定义域、值域、单调性和凸凹及极限等性质，函数的图像示意图如下：

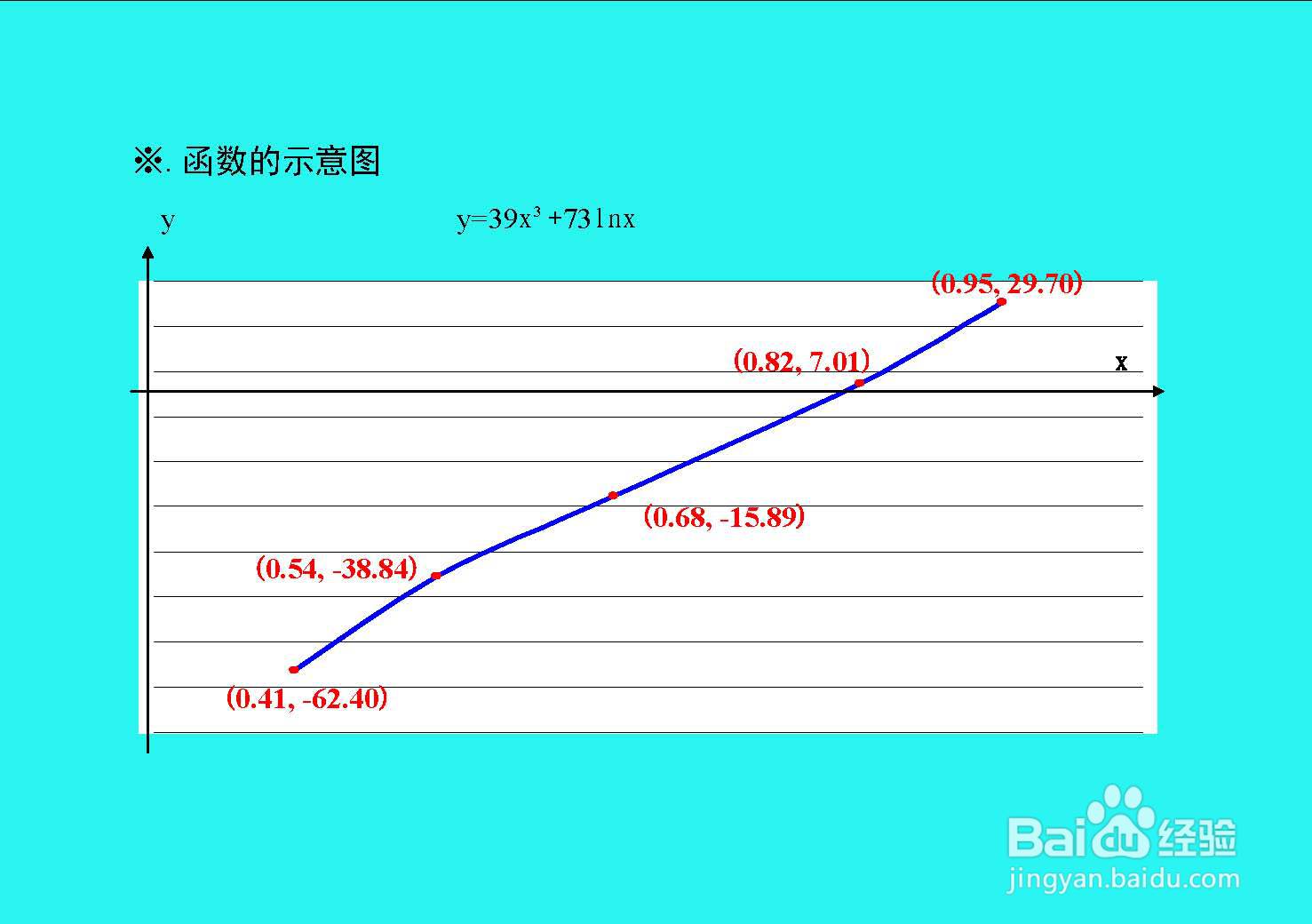END