本经验主要介绍八年级的数学之一次函数，共计练习题八道，其中选择题3道、填空题3道，计算题2道，分别解析其解题思路和主要计算步骤。

主要方法与步骤

1

点p(-32,62)在平面直角坐标系所在的象限为（ ）。

A.第一象限 B.第二象限 C.第三象限 D.第四象限

解题思路：根据直角坐标系内任意点P(a，b)横坐标和纵坐标的符号关系可知，当a＞0，b＞0时，点p在第一象限内；当a＜0，b＞0时，点p在第二象限内；a＜0，b＜0时，点p在第三象限内；a＞0，b＜0时，点p在第四象限内。对于本题，因为-32＜0，62＞0，所以该点p(-32,62)在第二象限内，故选择答案B。



2

点(49,-50)到y轴的距离是（ ）。

A. 49 B. 50 C.-50 D.- 49

解题思路：本题考察的距离知识点，因距离为非负数，所以答案C和D可以排除，又因为本题是求点到y轴的距离，即距离为点的横坐标的绝对值，由于横坐标为49＞0，所以本题点(49,-50)到y轴的距离是49，即选择A.



3

点(57x-48, 9x+2)在y轴上，则点的坐标为 。

解题过程：因为点在y轴上，所以横坐标为0，即有57x-48=0，可求出x=16/19，进一步代入纵坐标有：9x+2=9*16/19+2=182/19，则本题所求点的坐标为：(0, 182/19)。



4

已知一次函数y=7x+26-2a.

(1)若函数图像与y轴的交点在位于y轴的负半轴，则a的取值范围为 ；

(2)若-44≤x≤44，函数y的最大值为326，则a的值为 。

解题步骤：

(1)一次函数y=7x+26-2a与y轴的交点在y轴的负半轴，即x=0处时，有函数值y＜0，即：7*0+26-2a＜0，则2a＞26，所以a＞13。

(2)一次函数的单调性取决于自变量系数，对于一次函数y=ax+b，当系数a为正数时，函数y为增函数，当系数a为负数时，函数y为减函数。对于本题a=7＞0，故本题一次函数y=7x+26-2a为增函数，则函数最大值在x取到最大值时达到，所以：7*44+26-2a=326，即2a=8，则a=4.



5

一次函数经过点A(-9, 18)，B(46, 34)两点，求函数的表达式。

解：方法一：方程计算法

设该一次函数表达式为y=kx+b,根据题意两点在图像上，则有方程：

18=-9k+b;

34=46k+b.

两方程相减有：34-18=(46+9)k，则k=16/55.

代入其中一个方程有：

34=16/55*46+b，即可求出b=1134/55,

所以一次方程的表达式为：y=16x/55+1134/55。

方法二：直线方程点斜式计算

根据题意，图像经过A,B两点，则该直线的斜率k为：

k=(34-18)/[46-(-9)]=16/55.

则直线的方程为：

y-18=16/55(x+9)。



6

已知函数y-20与1x+8成正比例，且当x=-6时，y=22。

(1)求y与x的函数关系式。

(2)求函数y与两坐标轴围成的面积。

解：(1)根据题意，设比例系数为k，有：

y-20=k(1x+8),

将点x=-6，y=22代入有：

22-20=k(-1*6+8)，即k=1/1,

此时函数关系式为：

y-20=1/1(1x+8),

即y=1x/1+28/1.



7

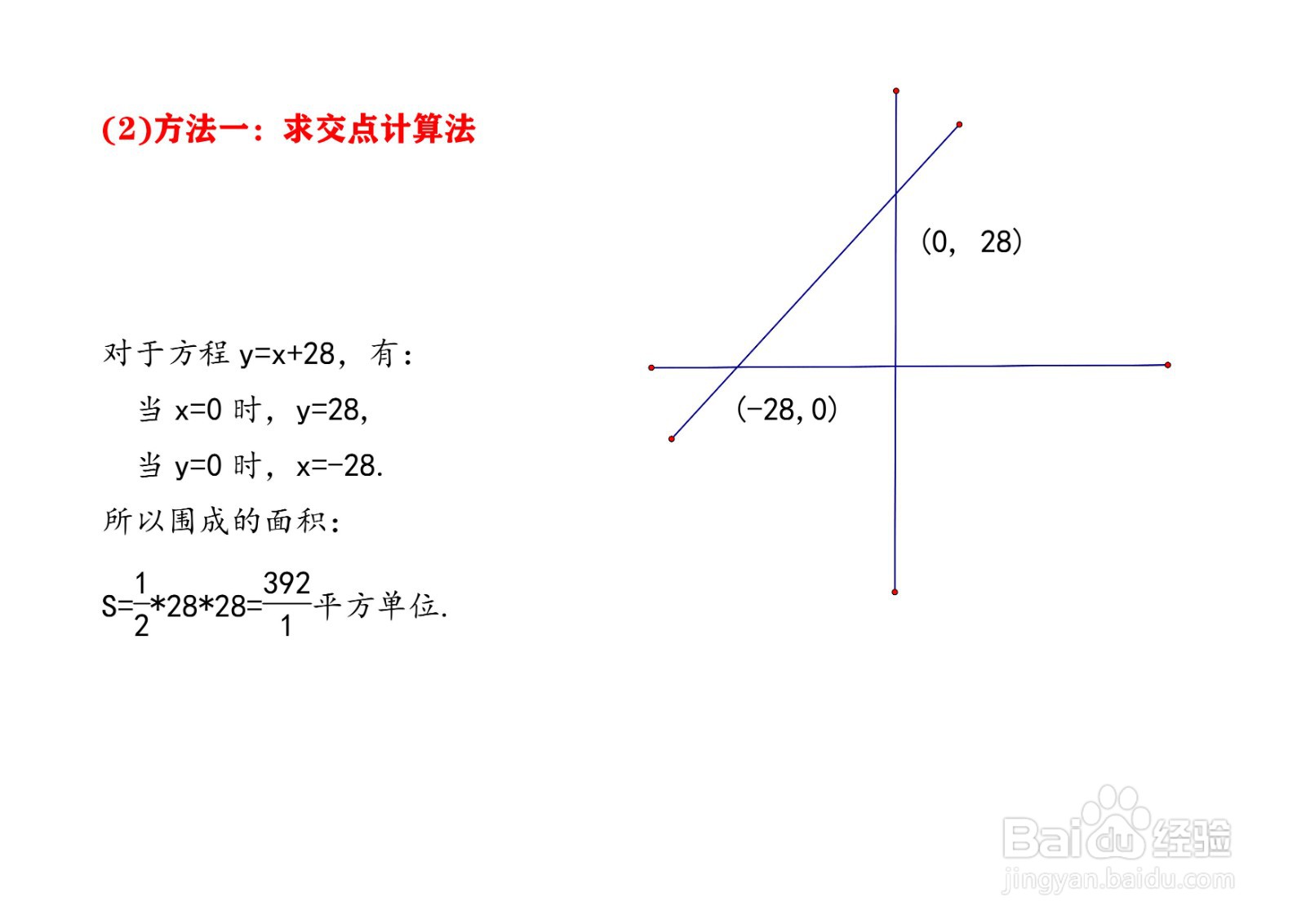
(2)方法一：求交点计算法

对于方程y=1x/1+28/1，有：

当x=0时，y=28/1,

当y=0时，x=-28/1.

所以围成的面积S=(1/2)* 28/1*28/1=392/1平方单位.



8

方法二：方程截距计算法

y=1x/1+28/1，

y-1x/1=28/1,

y/(28/1)-x/28/1=1,

即方程在y轴、x轴上的截距分别为28/1，-28/1,

所以围成的面积S=(1/2)* 28/1*28/1=392/1平方单位.

END